The elastic moduli express in mathematical form the ability of a material to temporarily deform under stress.

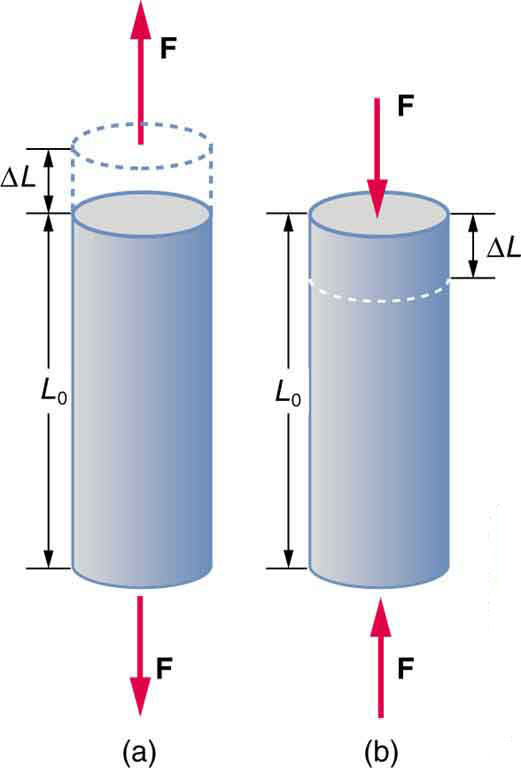
Hooke’s Law shows the relationship between stress and linear strain (usually represented by ε) through a constant which depends on the body under strain (σ = Eε). This constant is one of the elastic moduli, the Young’s Modulus (E), defined as the ratio of the stress σ along an axis on the deformation (ε) along the same axis:

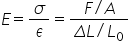
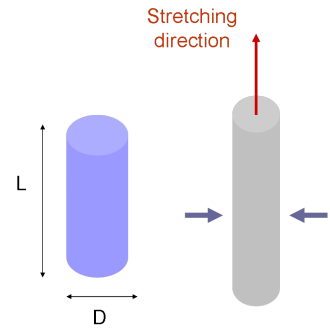
Poisson’s Ratio (ν) is the radial strain to axial strain ratio (when a material is compressed along a direction it usually tends to expand in another direction):

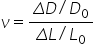
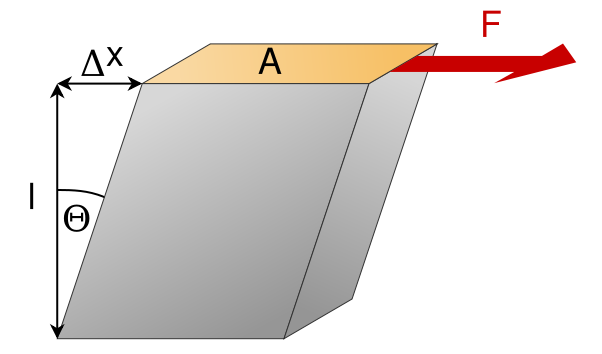
The Rigidity Modulus (μ), or shear modulus, is the ratio between shear stress τand shear strain (it is also known as Lamé’s 2nd constant):

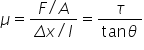
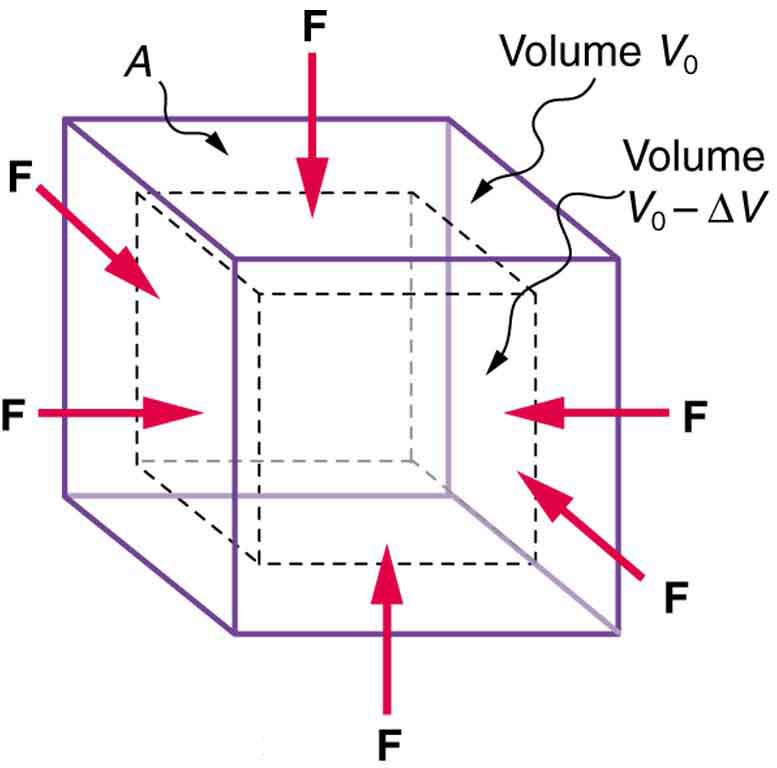
The Compressibility Modulus L (or Bulk Modulus) expresses the volume change following a deformation or strain:

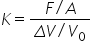
Lamé’s 1st constant λ relates the Bulk Modulus K with the shear modulus μ (Lamé’s 2nd constant):

hence:

 

< Stress and strain	Types of strain >